

We would need to know a few terms so that we could calculate the common difference and ultimately the formula for the general term. To do so, we would need to know two things. It may be necessary to calculate the number of terms in a certain arithmetic sequence. Uizmaster: Finding Formula for General Term Ideo: Finding the nth Term of an Arithmetic Sequence Now, we can use this formula to find its 14th term, like so. We can substitute this information into the explicit rule.

Now if we were asked to find the 37th term in this sequence, we would calculate for a 37 like this.Įxample 2: Find a formula that defines the nth term for sequence B. We can substitute this information into the explicit rule a n = a 1 + (n - 1)d, like so. The fixed number, called the common difference or d-value, is 3. If we match each term with it's corresponding term number, we get: Let us also look at the following examples.Įxample 1: Let's examine sequence A so that we can find a formula to express its nth term. To find these formulas, we will use the explicit rule. The formula can be used to find any term we with to find, which makes it a valuable formula. The d-value is 4 because it is the common difference. Our n-value is 724 because that is the term number we want to find. So, if we want to find the 724th term, we can use this explicit rule. What if we have to find the 724th term? This method would force us to find all the 723 terms that come before it before we could find it. 23 + 4 = 27 so, 27 is the 7th number in the sequence, and so on. So, 23 is the 6th number in the sequence. To find the next number after 19 we have to add 4. We can see the common difference is 4 no matter which adjacent numbers we choose from the sequence. Let us say we were given this arithmetic sequence.įirst, we would identify the common difference. The recursive rule means to find any number in the sequence, we must add the common difference to the previous number in this list. To determine any number within an arithmetic sequence, there are two formulas that can be utilized. When we subtract any two adjacent numbers, the right number minus the left number should be the same for any two pairs of numbers in an arithmetic sequence. Remember, the letter d is used because this number is called the common difference. where n is any positive integer greater than 1. The d-value can be calculated by subtracting any two consecutive terms in an arithmetic sequence. This notation is necessary for calculating nth terms, or a n, of sequences. This means that if we refer to the fifth term of a certain sequence, we will label it a 5.

Mathematicians also refer to generic sequences using the letter a along with subscripts that correspond to the term numbers as follows: Mathematicians use the letter d when referring to these difference for this type of sequence.
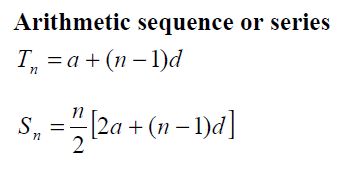
So that we can examine these sequences to greater depth, we must know that the fixed numbers that bind each sequence together are called the common differences.
Sequences and series formulas plus#
The fourth number plus -2 is the fifth number: 14 + (-2) = 12.īecause these sequences behave according to this simple rule of addiing a constant number to one term to get to another, they are called arithmetic sequences. This too works for any pair of consecutive numbers. Sequence C is a little different because we need to add -2 to the first number to get the second number. The third number plus 5 is the fourth number: 36 + 5 = 41, which will work throughout the entire sequence. This also works for any pair of consecutive numbers. The second number plus 3 is the third number: 8 + 3 = 11, and so on.įor sequence B, if we add 5 to the first number we will get the second number. This works for any pair of consecutive numbers. įor sequence A, if we add 3 to the first number we will get the second number. The following sequences are arithmetic sequences: Sequence A: 5, 8, 11, 14, 17. Sequences of numbers that follow a pattern of adding a fixed number from one term to the next are called arithmetic sequences.


 0 kommentar(er)
0 kommentar(er)
